1.雅可比（jacobi）迭代

1.1 迭代格式

$$

$$

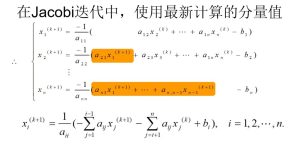
1.2 例题

$$

$$

2.高斯赛德尔迭代法

2.1 迭代格式

$$

$$
高斯赛德尔迭代法在雅可比迭代中使用刚刚迭代出来的值。

3.2迭代矩阵

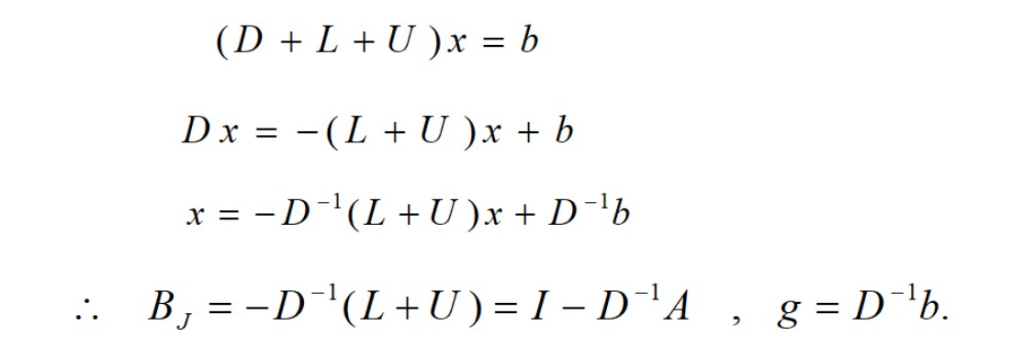
2.2 例题

高斯赛德尔：
$$

$$

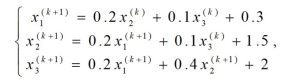
1）迭代法不存在累积误差问题。
2）GS迭代法的收敛速度一般比J迭代法快。两种迭代法可能都收敛，可能都不收敛；也有可能是GS迭代收敛而J迭代不收敛；但亦有相反情形，即J迭代收敛而GS迭代不收敛。

3.逐步超松弛迭代

3.1 迭代格式

3.2迭代矩阵

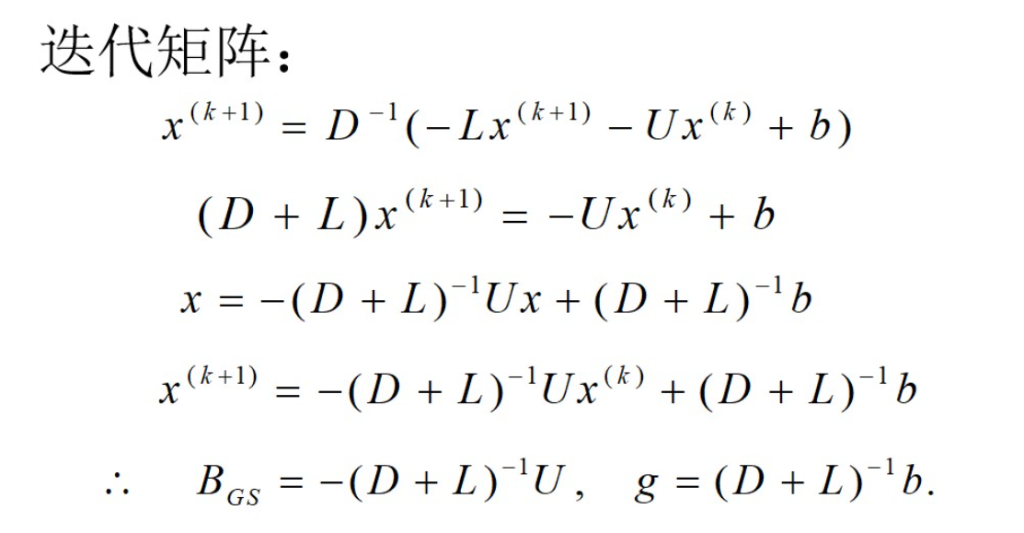
4.例题及代码

例题：

代码：

#include<iostream>
#include<cstdlib>
#include<cmath>
using namespace std;
double matrix[3][3]={{0,-0.75,0},{-0.75,0,0.25},{0,0.25,0}};//已经约分过的矩阵，jacobi和gs中用到
double matrix2[3][3]={{4,3,0},{3,4,-1},{0,-1,4}};//未修改过的系数矩阵，jacobi和gs中用到
double end_m[]={6,7.5,-6};//约分后的向量，用在逐步超松弛迭代
double b[3]={24,30,-24};//未修改的b向量，用在逐步超松弛迭代
int count=1;
void jacobiFunction(double *xk,double *xk1);//雅可比迭代
bool isEqual(double *xk,double *xk1);
void gsFunction(double xk[],double *xk1);//高斯赛德尔迭代法
void sorFunction(double xk[],double omiga,double *xk1);//逐步超松弛迭代
void xk1Toxk(double *xk,double *xk1);
void resetXK(double *xk,double *xk1);
void printXK(double *xk);
int main(){
    double xk[]={1,1,1};//迭代初始值，x1,x2,x3初始值
    double xk1[]={0,0,0};//下一次迭代结果，迭代后得到的下一次结果
    cout<<"jacobi:"<<endl;
    //for循环设置迭代次数20,防止死循环，输出每次的迭代结果
    for(int i=0;i<100;i++){
        jacobiFunction(xk,xk1);
        xk1Toxk(xk,xk1);
        printXK(xk);
        count++;
    }
    resetXK(xk,xk1);
    count=1;
    cout<<endl<<"高斯-塞德尔:"<<endl;
    //for循环设置迭代次数20,防止死循环，输出每次的迭代结果
    for(int i=0;i<20;i++){
        gsFunction(xk,xk1);
        // if(isEqual(xk,xk1)){
        //     break;
        // }
        xk1Toxk(xk,xk1);
        printXK(xk);
        count++;
    }
    resetXK(xk,xk1);
    count=1;
    cout<<endl<<"sor:(omigo=1.8)"<<endl;
    //for循环设置迭代次数20,防止死循环，输出每次的迭代结果
    for(int i=0;i<20;i++){
        sorFunction(xk,1.8,xk1);
        // if(isEqual(xk,xk1)){
        //     break;
        // }
        xk1Toxk(xk,xk1);
        printXK(xk);
        count++;
    }
    resetXK(xk,xk1);
    count=1;
    cout<<endl<<"sor:(omigo=1.22)"<<endl;
    //for循环设置迭代次数10,防止死循环，输出每次的迭代结果
    for(int i=0;i<10;i++){
        sorFunction(xk,1.22,xk1);
        // if(isEqual(xk,xk1)){
        //     break;
        // }
        xk1Toxk(xk,xk1);
        printXK(xk);
        count++;
    }

}
//雅可比迭代格式函数
void jacobiFunction(double xk[],double *xk1){
    for(int i=0,j=0;i<3;i++){
        for(j=0;j<3;j++){
            //i!=j是即不加上Xii这一项
            if(i!=j){
                *(xk1+i)+=matrix[i][j]*xk[j];
            }
        }
        *(xk1+i)+=end_m[i];//加上约分后的最后一个向量的值
    }
}
//高斯赛德尔迭代法
void gsFunction(double xk[],double *xk1){
    for(int i=0,j=0;i<3;i++){
        for(j=0;j<3;j++){
            if(i!=j){
                *(xk1+i)+=matrix[i][j]*xk[j];
            }
        }
        *(xk1+i)+=end_m[i];
        xk[i]=*(xk1+i);//将每一次迭代的结果给xk,参与下一次迭代
    }
}

//逐步超松弛迭代
void sorFunction(double xk[],double omiga,double *xk1){
    for(int i=0,j=0;i<3;i++){
        double sum=0;
        sum+=b[i];
        for(j=0;j<3;j++){
            sum-=matrix2[i][j]*xk[j];
        }
        *(xk1+i)=xk[i]+omiga*sum/matrix2[i][i];//sum乘与w/aii，sum是迭代格式中最后的括号内的值。
        xk[i]=*(xk1+i);
    }
}

//以下是程序其它函数
void resetXK(double *xk,double *xk1){
    for(int i=0;i<3;i++){
        *(xk+i)=1;
        *(xk1+i)=0;
    }
}
void printXK(double *xk){
    cout<<"第"<<count<<"次迭代:"<<"x1,x2,x3="<<*(xk+0)<<" "<<*(xk+1)<<" "<<*(xk+2)<<endl;
}
void xk1Toxk(double *xk,double *xk1){
    for(int i=0;i<3;i++){
        *(xk+i)=*(xk1+i);
        *(xk1+i)=0;
    }
}
bool isEqual(double *xk,double *xk1){
    for(int i=0;i<3;i++){
        if(fabs(*(xk+i) - *(xk1+i)) > std::numeric_limits<double>::epsilon()){
            return false;
        }
    }
    return true;
}

结果：

jacobi:
第58次迭代:x1,x2,x3=3 4 -5
高斯赛德尔迭代:
第24次迭代:x1,x2,x3=3 4 -5
逐步超松弛迭代:
omigo=1.8:
第64次迭代:x1,x2,x3=3 4 -5
omigo=1.22:
第10次迭代:x1,x2,x3=3 4 -5