1.原理
1.1 差商
平均变化率:

1.2 牛顿插值公式
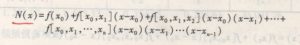
2.Python代码
x=[-1,0,2,3]
y=[-4,-1,0,3]
求f(1.5)的值:
def dqtable(x,data):
#计算差商表
for i in range(1, len(x)):
f = []
for k in range(len(x) - i):
k = -(k+1)
c = (data[i-1][k]-data[i-1][k-1])/(x[k] - x[k - i])
f.append(c)
f.reverse()
data.append(f)
return data
def getEnd(x_f,x,data):
end=0
# 依次通过差商表计算结果
for i in range(len(data)):
upper = 1
for j in range(i):
upper *= (x_f - x[j])
end += data[i][0] * upper
return end
# 存放自变量x的值 data 用于存放函数值以及差商
x=[-1,0,2,3]
data = [[-4,-1,0,3]]
# 用于存放待求值点以及计算结果
x_f = 1.5
fun = 0
data=dqtable(x,data)
print('第一题:')
print("差商表:",data)
fun=getEnd(x_f,x,data)
print('点 {} 在此函数的插值结果为:{}'.format(x_f,fun))插值多项式绘图:
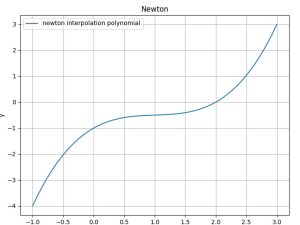
#画牛顿插值多项式
import matplotlib.pyplot as plt
import numpy as np
#从-1,3中取50个点,计算插值多项式的值并画图
x1=np.linspace(-1, 3,50)
y1=[]
for i in x1:
y1.append(getEnd(i,x,data))
print(y1[0:10])
plt.figure(figsize=(8, 6))
plt.plot(x1,y1,label='newton interpolation polynomial')
plt.legend()
plt.title("Newton")
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.show()结果: